Los ángulos y sus tipos varían dependiendo de los grados (°) que posean. De esta manera, es posible clasificarlos en:
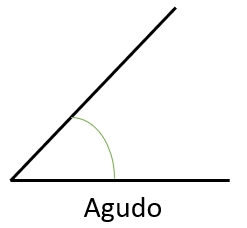
1) Ángulo agudo: es aquel que mide más de 0° y menos de 90°.
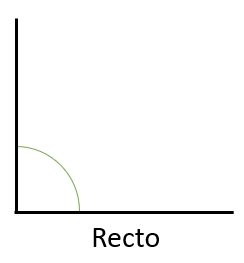
2) Ángulo recto: es aquel que mide 90°.
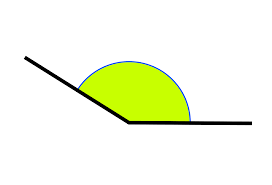
3) Ángulo obtuso: es aquel que mide más de 90° y menos de 180°.
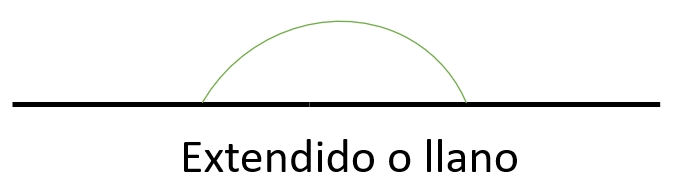
4) Ángulo extendido: es aquel que mide 180°.
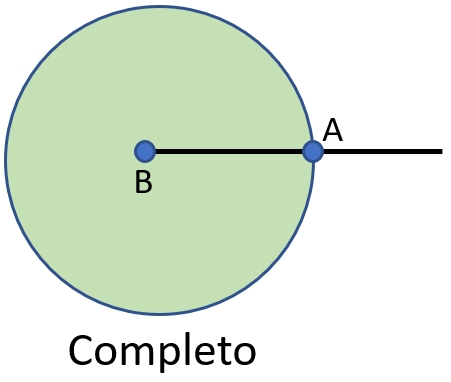
5) Ángulo completo: es aquel que mide 360°.
Tipos de ángulos
1) Ángulos suplementarios:
Un ángulo es suplementario de otro ángulo cuando la suma de sus medidas da como resultado un ángulo extendido.

2) Ángulos complementarios:
Un ángulo es complementario de otro ángulo cuando la suma de sus medidas da como resultado un ángulo recto.

3) Ángulos opuestos por el vértice:
Dos ángulos son opuestos por el vértice cuando tienen un vértice en común y sus lados son semirrectas opuestas. Los ángulos opuestos por el vértice tienen igual medida, ya que tienen igual amplitud.

4) Ángulos adyacentes:
Dos ángulos son adyacentes cuando tienen un lado en común y el otro lado está formado por dos semirrectas opuestas. Los ángulos adyacentes son siempre suplementarios, ya que su suma es igual a 180°.

5) Ángulos formados por rectas paralelas cortadas por una transversal:
Si intersectamos dos rectas paralelas por una transversal, obtendremos 8 ángulos, 4 en cada punto de intersección.

Son ángulos correspondientes, aquellos que tienen la misma ubicación en ambos grupos de 4 ángulos. En el caso de dos rectas paralelas cortadas por una transversal, los ángulos correspondientes tienen la misma medida.

Además, se forman ángulos opuestos por el vértice, que como aprendimos anteriormente, tienen igual medida.

Si tenemos dos rectas paralelas cortadas por una transversal, podemos concluir entonces que:

Veamos un ejemplo:
Tenemos dos rectas paralelas cortadas por una transversal.
Si el ángulo 1 mide 60°, ¿podemos saber la medida de todos los demás ángulos?

El ángulo 2 mide 120°, ya que, es suplementario del ángulo 1, por lo tanto:
Ángulo 1 + ángulo 2 = 180°
Como el ángulo 1 mide 60°, entonces, el ángulo 2 mide 120°.
El ángulo 3 mide 60°, ya que, los ángulos 1 y 3 son opuestos por el vértice, por lo tanto, tienen la misma medida. Además, el ángulo 3 es suplementario del ángulo 2, por lo tanto, ambos miden 180°; y si el ángulo 2 mide 120°, entonces el ángulo 3 mide 60°.
El ángulo 4 mide 120°, ya que, los ángulos 2 y 4 son opuestos por el vértice y además el ángulo 4 es suplementario tanto del ángulo 3 como del ángulo 1.
Luego, podemos obtener las medidas de los ángulos 5, 6, 7 y 8.
El ángulo 5 mide mide 60°, ya que, es correspondiente con el ángulo 1.
El ángulo 6 mide 120°, ya que, además de ser correspondiente con el ángulo 2, es suplementario del ángulo 5.
El ángulo 7 mide mide 60°. El ángulo 7 es correspondiente con el ángulo 3, es suplementario con el ángulo 6 y opuesto por el vértice con el ángulo 5.
El ángulo 8 mide 120°. Es correspondiente con el ángulo 4; suplementario, tanto del ángulo 7 como del ángulo 5 y opuesto por el vértice con el ángulo 6.