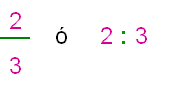Las razones puedes ser expresadas de dos maneras:
Cuando tenemos una igualdad entre dos razones, estamos frente a una proporción.
Acá te presentamos algunos ejemplos:

Para comprobar que se cumpla la igualdad entre dos razones, debemos multiplicar cruzado y si los productos son los mismos, entonces estamos frente a una proporción.
Veamos este ejemplo:

En toda proporción podemos distinguir dos variables.
Si al aumentar una variable, la otra también aumenta, entonces se trata de una proporción directa.
Ejemplo:
Para tejer 2 chalecos de niño se utilizarán 240 gramos de lana. Si queremos tejer 5 chalecos, ¿cuántos gramos de lana necesitaremos?
Primero debemos distinguir las variables: gramos de lana y número de chalecos.
Luego debemos preguntarnos: Si aumentamos los gramos de lana, ¿aumentarán los chalecos que podremos tejer?
La respuesta es sí. Como al aumentar una variable, también aumentará la otra, entonces la proporción es directa.
La proporción sería la siguiente:

Como puedes ver, en el caso de las proporciones directas, una variable la pondremos en el numerador, y la otra en el denominador.
Además los datos se pondrán en una misma razón como muestra la figura:

Resolvamos la proporción, multiplicando cruzado, para obtener la incógnita que necesitamos:

Necesitaremos 600 gramos de lana para tejer 5 chalecos de niño.
Cuando al aumentar una variable, la otra disminuye, estamos frente a una proporción inversa.
Ejemplo:
2 trabajadores construyen una cerca en 9 horas. Si contratamos 4 trabajadores más, ¿cuántas horas nos demoraremos en construir la cerca?
En este caso, las variables son: número de trabajadores y horas.
Si aumentamos el número de trabajadores, disminuirán las horas que demoraremos en construir la cerca.
Como al aumentar una variable, la otra disminuyó, entonces la proporción es inversa.
La proporción sería la siguiente:

En este tipo de proporciones, una variable la pondremos en la primera razón y la otra variable en la segunda.
Además, los datos se pondrán en forma cruzada como se muestra a continuación:

Resolvamos ahora la proporción para obtener la incógnita que buscamos:

Al aumentar los trabajadores de 2 a 6, disminuirán las horas de construcción de la cerca de 9 a 3 horas.
Veamos otros ejemplos:
1) Para recorrer 150 kilómetros necesitamos 1 350 litros de bencina. Si tenemos sólo 900 litros, ¿cuántos kilómetros podremos recorrer?
Al disminuir una variable, disminuyó también la otra, por lo tanto estamos frente a una proporción directa.

900 litros de bencina nos alcanzarán para recorrer 100 kilómetros.
2) Queremos etiquetar 1 200 productos. Con las las máquinas que tenemos podríamos etiquetarlos en 16 días. ¿Cuántas máquinas necesitaremos para que podamos lograrlo en sólo 4 días?
En este ejemplo, al aumentar el número de máquinas, lograremos etiquetar los productos en menos días, entonces es una proporción inversa.

Necesitaremos 8 máquinas para lograr etiquetar los 1 200 productos en 4 días.