Hay 3 tipos de transformaciones isométricas:
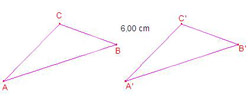
Traslación
Isometría determinada por un vector. La traslación tiene dirección, que puede ser horizontal, vertical u oblicua; sentido, que puede ser derecho, izquierdo, arriba y abajo; y magnitud, que es la distancia entre la posición inicial y la posición final de cualquier punto de la figura.
Veamos un ejemplo:

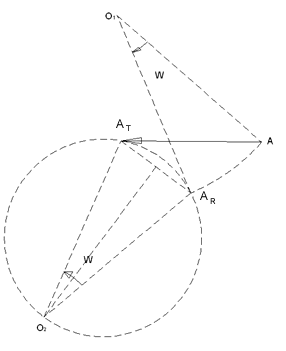
Rotación
Isometría en que todos los puntos giran un ángulo constante con respecto a un punto fijo, denominado centro de rotación. La cantidad de giro lo llamaremos ángulo de rotación.
Observemos:

Reflexión
Es una simetría que está determinada por una recta llamada eje de simetría.

La parte que está a la derecha del eje y es exactamente igual que la que está a la izquierda del mismo eje, por lo tanto, el eje y, es decir, el eje de las coordenadas, corresponde al eje de simetría.
La distancia de A a al eje y es igual a de la A´ al mismo eje. Lo mismo ocurre con los demás puntos de los triángulos.