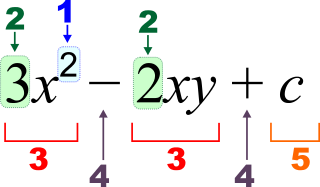
¿Quieres aprender a realizar una reducción de expresiones algebraicas de manera sencilla? Aprende a través de estos tres pasos.
Paso 1: análisis del problema
El primer paso es analizar el problemas, a fin de determinar si es posible simplificar o realizar la reducción de expresiones algebraica. Para ello, lo primero que debes hacer es identificar si existen términos semejantes.
Los términos semejantes son aquellos que tienen las mismas variables y exponentes. Por ejemplo: en la expresión 3x + 2y + 5x – 4y, los términos semejantes serían:
a) 3x + 5x,
b) 2y – 4y
Una vez que hayas identificado los términos semejantes, puedes combinarlos sumando o restando sus coeficientes.
En este ejemplo:
a) 3x + 5x = 8x
b) 2y – 4y = -2y
En una expresión algebraica, los términos semejantes son aquellos que tienen las mismas variables y exponentes.
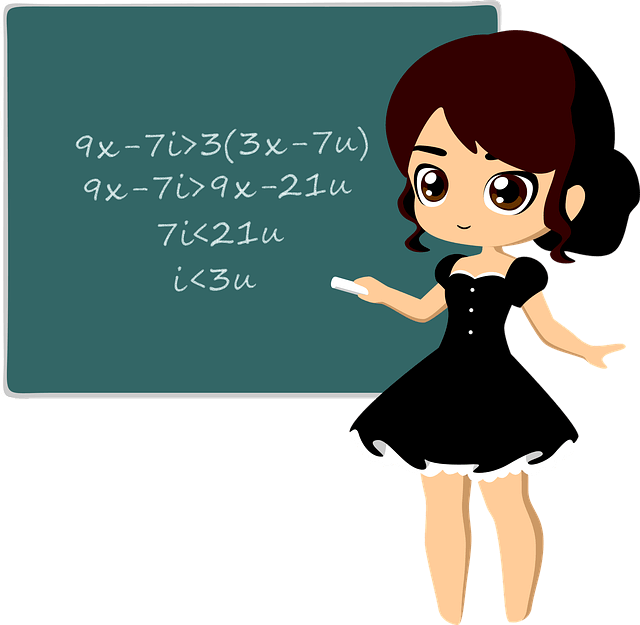
Reducción de expresiones algebraicas
Paso 2: simplificar
El segundo paso para simplificar una expresión algebraica es factorizar los términos comunes.
Esto significa encontrar el factor común más grande entre los términos de la expresión y sacarlo fuera de los paréntesis.
Por ejemplo, en la expresión 6x + 9, el factor común es 3, por lo que podemos factorizarla como 3(2x + 3).
Este paso ayuda a reducir la expresión y hacerla más fácil de manejar.
Paso 3: paréntesis y operaciones
Antes de simplificar una expresión algebraica, es importante realizar todas las operaciones matemáticas necesarias, como sumas, restas, multiplicaciones y divisiones.
Si hay paréntesis, se deben resolver primero. Luego de los paréntesis, debemos resolver las multiplicaciones y divisiones. Y por último, las sumas y restas.
El orden de resolución dentro de un problema matemático, se realiza de la siguiente manera:
- Paréntesis
- Potencias
- Multiplicaciones
- Divisiones
- Adición (Suma)
- Sustracción (Restas)
Es importante que analices el problema. En caso de que no existan términos semejantes, no se puede realizar una reducción de expresiones algebraicas.