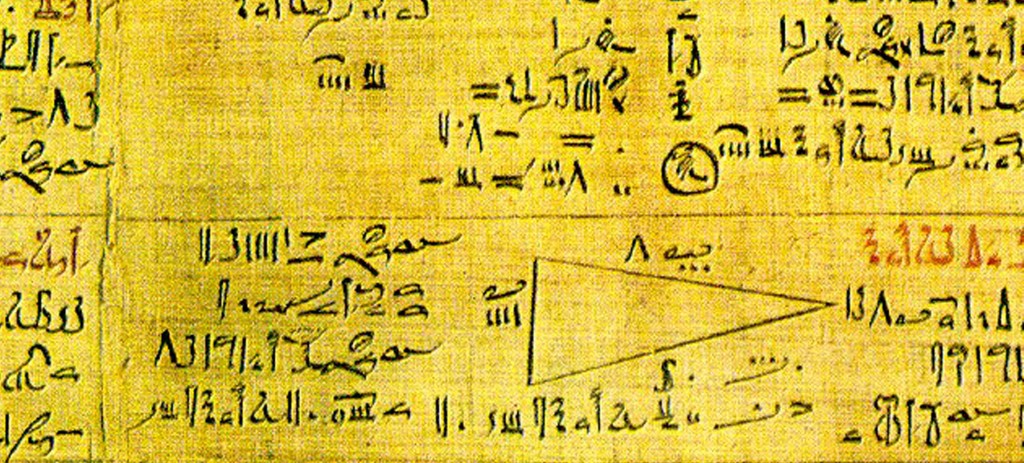
Los estudios matemáticos en el Antiguo Egipto tuvieron un origen práctico. Alcanzaron un gran nivel en las manipulaciones aritméticas pero sus métodos eran toscos y sin grandes generalizaciones. Casi no hay simbolismo y los egipcios eran poco dados a investigaciones abstractas. Trabajaron sobre todo en geometría y aritmética.
Desde el tercer milenio A.C. los egipcios crearon un sistema de numeración decimal, es decir contaban de 10 en 10, no tenían símbolo para el cero y utilizaban los geroglíficos (ver glosario) de la figura para representar los distintos ordenes de unidades.
El procedimiento era de tipo aditivo, es decir, las cifras eran repetidas. Así, por ejemplo, si el uno se escribía como una línea vertical, el cuatro era representado como cuatro líneas verticales. Un signo no se repetía más de nueve veces seguidas, ya que a la décima vez se utilizaba el número siguiente.
Se usaban tantos de cada uno cómo fuera necesario y se podian escribir indistintamente de izquierda a derecha, al revés o de arriba abajo, cambiando la orientación de las figuras según el caso.
Como no importaba el orden, se escribían a veces según criterios estéticos y solían ir acompañados de los geroglíficos correspondientes al tipo de objeto (animales, prisioneros, vasijas etc.) cuyo número indicaban.
Pero en un principio los egipcios escribían los nueve primeros números colocando símbolos de la unidad, uno a continuación de otro; más tarde utilizaron la representación por desdoblamiento mientras los arameos de Egipto usaban un principio ternario (ver tabla).
Estos signos fueron utilizados hasta la incorporación de Egipto al imperio romano. Pero su uso quedó reservado a las inscripciones monumentales, en el uso diario fue sustituido por la escritura hierática y demótica (ver glosario), formas más simples que permitian mayor rapidez y comodidad a los escribas.
En estos sistemas de escritura los grupos de signos adquirieron una forma propia, y así se introdujeron símbolos particulares para 20, 30…90…200, 300…900, 2000, 3000… con lo que disminuye el número de signos necesarios para escribir una cifra.
Estos jeroglíficos numéricos estaban reservados a las inscripciones sobre monumentos de piedra. Los escribas para realizar los documentos de tipo administrativo, astronómico, etc., fueron simplificando el trazo hasta obtener los llamados signos hieráticos. Por ejemplo el 20 en notación jeroglífica se escribía  , mientras en hierática se denotaba mediante
, mientras en hierática se denotaba mediante  .
.
El escriba o calculador egipcio realizaba operaciones aritméticas elementales, con números enteros y el uso casi exclusivo de fracciones unitarias. El papiro de Rhind contiene al principio una tabla en la que se expresan las fracciones de numerador 2 y de denominador impar entre 5 y 101, como suma de fracciones unitarias; con ellas efectuaban las cuatro operaciones aritméticas con fracciones.
La naturaleza de los números irracionales no llegó a reconocerse en la aritmética egipcia. Las raíces cuadradas sencillas que aparecían en los problemas se expresaban mediante números enteros y fracciones.
Glosario
– Jeroglífico: usado desde finales del Período predinástico (3 100 a.C.) hasta el S. IV d.C. Fue el sistema más empleado para escribir sobre las paredes de templos, tumbas y palacios.
– Hierático: del griego hieraticós «sacerdotal». Tuvo su origen en las formas cursivas y abreviadas de los caracteres jeroglíficos (jeroglífico cursivo) al escribirlos sobre papiros. También se conoce su utilización desde el Imperio Antiguo (3 000 a.C.) hasta el 470 d.C. Se usó, además, sobre otros soportes como la cerámica, madera, telas y papiros; este último fue el soporte más utilizado.
– Demótico: Del griego demoticós «popular», también conocida por los primeros egiptólogos como «encorial», del griego egjoórios «indígena, autóctono». Los egipcios la denominaban «escritura de documentos» (o documental). El demótico es una forma abreviada y modificada de la escritura hierática que al parecer comenzó a utilizarse a partir de la Dinastía Etiópica. En los tiempos de Ptolomeo fue usado como escritura para los asuntos de la vida cotidiana. Ocasionalmente se encuentra sobre estelas de piedras y estatuas, como en la célebre Piedra de Rosetta.
La naturaleza de los números irracionales no llegó a reconocerse en la aritmética egipcia. Las raíces cuadradas sencillas que aparecían en los problemas se expresaban mediante números enteros y fracciones.