¿Sabías que un 45% de los estudiantes comenten errores al resolver ejercicios de potencias? El principal error está en la forma de abordar los problemas y en no conocer qué son las potencias y sus propiedades.
A través de las estas cinco propiedades de las potencias con ejemplos, aprenderás a resolver todo tipo de problemas, sin importar cuál sea su grado de dificultad.
Antes de comenzar, debes saber que las potencias son un tipo de operación matemática en la cual existen dos términos: una base y un exponente. El primer término (base) corresponde al número que multiplicamos, mientras que el exponente nos indicará la cantidad de veces que se multiplicará.
Recuerda que para mejores resultados, debes seguir practicando hasta internalizar cada una de estas propiedades de la potenciación.

Propiedades de la potenciación
Un dato relevante que nunca debes olvidar cuando estés frente a un ejercicio, es que las potencias que tienen un exponente par, siempre darán como resultado un número positivo.
Estas son las potencias y sus propiedades:
1) Multiplicación de potencias de igual base
Al multiplicar potencias de igual base, mantendremos la base y sumaremos los exponentes.
Ejemplo:
2) División de potencias de igual base
Cuando queremos dividir potencias de igual base, mantendremos la base y restaremos los exponentes, de esta manera:
Ejemplo:
3) Potencia de una potencia
Para resolver la potencia de una potencia, debemos mantener la base y multiplicar los exponentes, de esta manera:
Ejemplo:
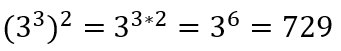
4) Multiplicación de potencias de igual exponente
Para obtener el producto de potencias de igual exponente, debemos multiplicar las bases y mantener el exponente, siguiendo el ejemplo:
Ejemplo:
5) División de potencias de igual exponente
Para obtener el cuociente de potencias de igual exponente, debemos dividir las bases y mantener el exponente, como indica la figura:
Ejemplo:
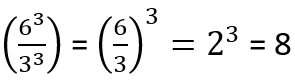
Como te habrás dado cuenta, las propiedades de las potencias son aplicables a bases naturales, fraccionarias, decimales y enteras.
Estas son las propiedades de la potenciación.
Ejemplos prácticos
- Encuentra el producto de la siguiente expresión: a5 × b3 × a8
Solución paso a paso:
- Analiza la expresión: a5 × b3 × a8
- Utiliza la regla de multiplicación de potencias de igual base: am × an = a(m+n)
- Agrupamos las incógnitas de igual base:
- a5 × b3 × a8
- = a5+8 × b3
- = a13 × b3
- = a13b3
2. Simplifiquemos la siguiente expresión: p12 ÷ p4q
Analizamos la expresión p12 ÷ p4q
Para simplificar utilizaremos la regla de cociente o división de potencias: am/an = am-n
- p12/p4q
- = p12-4/q
- = p8/q
De esta manera: p12 ÷ p4q nos dará como resultado:
= p8/q
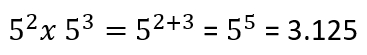
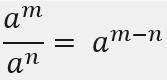
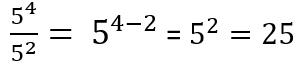
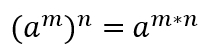







 Batalla de Lircay
Batalla de Lircay