Los poliedros regulares corresponde a figuras tridimensionales limitada por 4 o más polígonos.
Existen cinco poliedros regulares conocidos, los cuales también son llamados sólidos platónicos.
Estos son:
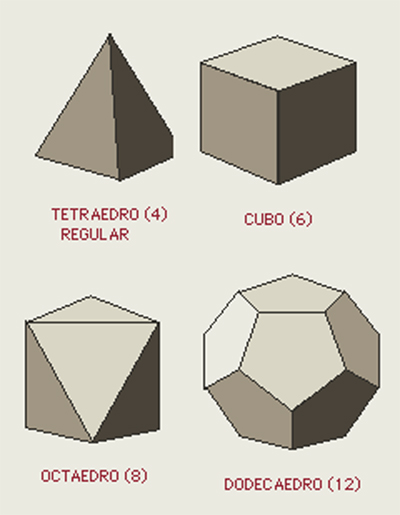
- Tetraedro (4 caras triangulares)
- Cubo (6 caras cuadradas)
- Octaedro (8 caras triangulares)
- Dodecaedro (12 caras pentagonales)
- Icosaedro (20 caras triangulares)
Entre las principales características de los poliedros regulares se encuentran:
- Todos tienen caras poligonales regulares. Esto significa que todos los lados y los ángulos de las caras son iguales.
- En cada vértice se encuentran el mismo número de caras.
- El mismo número de aristas se encuentra en torno a cada vértice.
¿Cuáles son los poliedros regulares?
¿Cómo calcular el número de caras, vértices y aristas en un poliedro regular?
Para calcular las caras, ángulos y aristas de un poliedro regular, existen distintas fórmulas.
Sin embargo, estas son las más utilizadas:
- Para calcular el número de caras (C): Se divide el número total de aristas (A) entre el número de lados de cada cara (n): C = A / n.
- Para calcular el número de vértices (V): se puede calcular dividiendo el número total de aristas (A) entre el número de aristas que se encuentran en cada vértice (k): V = A / k.
- Para calcular el número de aristas (A): se puede calcular multiplicando el número de vértices (V) por el número de aristas que se encuentran en cada vértice (k): A = V * k.