El Teorema de Pitágoras surge en la antigüedad, si nos detenemos a observar las construcciones antiguas, notaremos que los constructores tuvieron que hacer ángulos rectos sin mayores instrumentos.
Se supone que usaban cuerdas en la cual hacían nudos a igual distancia, al doblar la cuerda dos veces, dejando tres nudos, cuatro nudos y cinco nudos, formaban un triángulo rectángulo.
Qué es el teorema de Pitágoras
En palabras simples, el teorema de Pitágoras describe la relación que existe entre los lados de un triángulo rectángulo.
El teorema destaca que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado más largo de la figura) es igual a la suma de los cuadrados de los otros dos lados.
¿Cómo se expresa matemáticamente? El teorema de Pitágoras se expresa así:
c^2 = a^2 + b^2, en donde «c» es la hipotenusa y «a» y «b» son los otros dos lados de la figura.
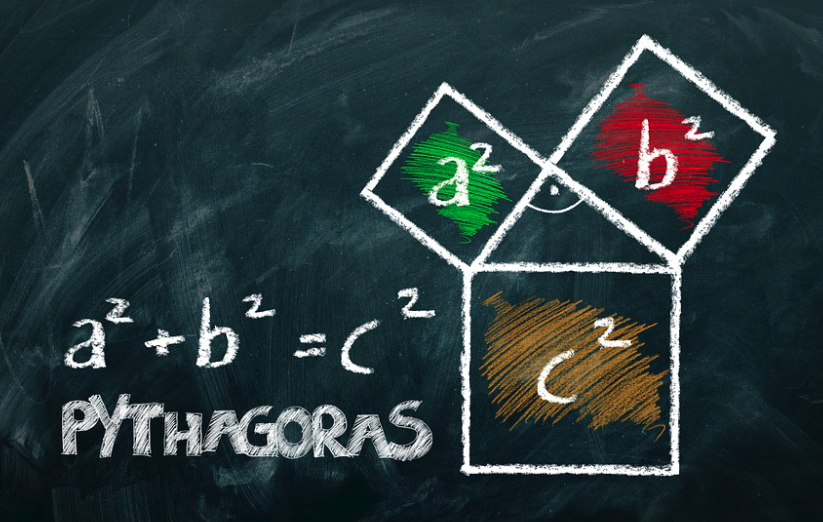
En la actualidad, ¿en qué se usa?
Este teorema es fundamental en la geometría y se utiliza en una amplia variedad de aplicaciones, desde la construcción de edificios hasta la resolución de problemas de física y astronomía.
Fue descubierto por el matemático griego Pitágoras y su escuela en la isla de Samos en el siglo VI a.C. y sigue siendo relevante en la actualidad.
Calcular la distancia entre una escalera y un muro

Imagina que estás frente a un muro que mide 2,70 metros de alto y quieres instalar una escalera con una separación de 70 cm, para evitar caer al suelo.
¿Cómo podemos calcular la longitud de la escalera?
- Debes establecer el ángulo recto entre la muralla y el suelo;
- Con la información de la altura de la pared (2,70 metros), junto a la separación entre el muro y la escalera a nivel del piso (70 cm), se definen los catetos;
- Imagina que la escalera es la representación gráfica de la hipotenusa.
Ahora, comencemos utilizando la formula, donde la variable «c» corresponde a la hipotenusa:
![]()
Para este ejercicio, las incógnitas «a» y «b» serán los catetos.
Despejamos:
![]()
Respondiendo a la pregunta, la escalera deberá tener, al menos, una altura de 279 cm para superar el borde de la pared.
¿A qué distancia de la tierra se encuentra el barco si se sabe que la distancia del barco a la parte superior del faro es 25 metros y, además, está 20 metros sobre el nivel del mar?
Conocidos los valores de a y c:
a = 25
c = 20
En este caso despejaremos «b», la cual corresponde a la incógnita. Vamos paso a paso:
![]()
Utilizamos los valores antes encontrados:
![]()
Con los valores descubiertos, ahora despejamos b^2 («b» elevado al cuadrado). Para ello, note como el número elevado se convierte en raíz del otro lado:
![]()
![]()
![]()
Ahora respondemos a la interrogante. ¿A qué distancia de la tierra se encuentra el barco?
La distancia de la tierra se encuentra el barco es de 15 metros.