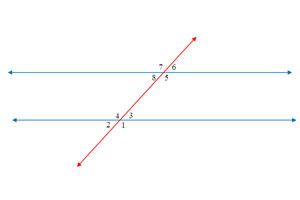
Recordaremos los ángulos que se forman en las paralelas cortadas por una transversal:
Son ángulos alternos interno < 3 con < 8 y < 4 con < 5
Son ángulos alternos externo < 1 con < 7 y < 2 con < 6
Son ángulos opuestos por el vértice < 1 con < 4 y < 2 con < 3
< 5 con < 7 y < 8 con < 6
Son ángulos correspondientes < 1 con < 5 y < 2 con < 8
< 3 con < 6 y < 4 con < 7
Todos estos ángulos son congruentes, es decir tienen la misma medida.
En la figura L1 es paralela a L2
ABC es triángulo.
AC y BC son transversales
Ocurre entonces que la medida <1 = medida <2 y medida <3 = medida <4
Podemos concluir entonces que:
medida <1 + medida <2 + medida <3 = 180°, ya que están sobre una misma recta.
Podemos concluir entonces que la suma de los ángulos interiores de un triángulos es 180°.
Cuadrilátero: En todo cuadrilátero convexo la suma de sus ángulos interiores es siempre 180°.
Todo cuadrilátero convexo se puede dividir en dos triángulos, veamos las siguientes figuras:
Se forman en esta figura dos triángulos y en cada uno de estos triángulos la suma de los ángulos interiores es 180°, podemos concluir que la suma de los ángulos interiores es 360°.
* Si te interesó este tema, te recomendamos visitar el siguiente artículo relacionado:
http://www.vitutor.com/geo/eso/el_5.html
