Sabemos que para poder determinar la probabilidad de ocurrencia de un evento es necesario conocer el espacio muestral y específicamente su cardinalidad.
Una de las técnica de conteo es el principio multiplicativo, el cual se usa para determinar la cardinalidad de un espacio muestral, es una forma de contar eficientemente.
Pensemos en el lanzamiento de dos dados:
En el primer lanzamiento tenemos 6 posibilidades, y en el segundo tenemos las mismas 6 posibilidades. Entonces tendremos en total 6·6=36 posibilidades.
Ahora bien, si tenemos 3 pantalones y 4 camisetas ¿Cuántas tenidas distintas podemos formar? 3·4=12 Posibles tenidas.
Es decir si tenemos un experimento el cual puede ocurrir de «n» maneras diferentes, un segundo experimento que tiene «m» maneras diferentes y el experimento es uno seguido del otro entonces tenemos n·m posibilidades de que este pueda ocurrir.
Este principio puede generalizarse a cualquier número de experimentos.
Para hacerlo más claro podemos ayudarnos con diagrama del árbol, veamos cómo lo podemos construir:
Veremos el caso del lanzamiento de los dados:
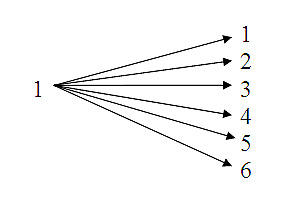
Supongamos que en el primer lanzamiento se obtiene 1, en el segundo lanzamiento podemos obtener 1, 2, 3, 4, 5, 6 lo representamos y obtenemos:
Segundo lanzamiento:

Tenemos por lo tanto 36 posibilidades.
Si te interesó el tema, te recomendamos el siguiente link: http://www.itch.edu.mx/academic/industrial/sabaticorita/_private/09Digramas%20de%20arbol.htm