En los siguientes ejercicios se muestran cómo desde un ejercicio simple, se desarrollan dis-tintas habilidades. Veamos un ejemplo para 7° Básico, utilizando el siguiente OF y CMO
O.F.: Comprender el teorema de Pitágoras y aplicarlo en situaciones concretas.
C.M.O.: Verificación, en casos particulares, en forma manual o mediante el uso de un procesador geométrico del teorema de Pitágoras, del teorema recíproco de Pitágoras y su apli-cación en contextos diversos.
EJEMPLO 1
El triángulo ABC, es rectángulo en C, entonces, el teorema de Pitágoras afirma que:
Habilidad Cognitiva:
Reconocimiento: Requiere del postulante la capacidad de reconocer hechos específicos; captar el sentido de terminologías propias de la matemática; reconocer algoritmos y proce-dimientos rutinarios; reconocer distintas maneras de expresar números; transformar en for-ma rutinaria elementos de una modalidad a otra, etc.
EJEMPLO 2
 ¿Cuánto mide (aproximadamente) el árbol, si la niña está a 8 metros de la base y la dis-tancia de la niña a la parte superior del árbol es 15 metros?
¿Cuánto mide (aproximadamente) el árbol, si la niña está a 8 metros de la base y la dis-tancia de la niña a la parte superior del árbol es 15 metros?
12,7 metros
64 metros
17 metros
289 metros
Otro valor
Habilidad Cognitiva:
Aplicación: Requiere del postulante la capacidad para aplicar los conocimientos matemáti-cos tanto a situaciones conocidas como a problemas relativamente nuevos y a otros desco-nocidos. En este contexto, el postulante debe ser capaz de utilizar diversas estrategias para resolver problemas; realizar comparaciones a la luz del problema; resolver problemas de rutina; descomponer y organizar información que se presenta en diversas formas; elaborar información necesaria para resolver un problema; etc.
EJEMPLO 3
Las dimensiones de una caja rectangular son 8cm de largo, 6 cm de ancho y 7cm de alto. Entonces la medida (aproximada) de la diagonal de la caja es:
10 cm
41 cm
12,2 cm
149 cm
Otro valor
Habilidad Cognitiva:
ASE (Análisis, Síntesis, Evaluación): Requiere del postulante la capacidad para analizar, realizar síntesis y evaluar. Estos son los procesos cognitivos superiores, es decir, aquí el grado de complejidad es mayor que en las categorías anteriores. En forma particular corres-ponde, entre otras, a la capacidad para inferir relaciones que se dan entre los elementos de un problema; descubrir patrones y regularidades; sacar conclusiones a partir de una infor-mación dada; efectuar abstracciones de figuras geométricas, gráficos y diagramas, para resolver problemas; y evaluar la pertinencia de las soluciones de un problema.
* Si te interesó este tema, te recomendamos visitar el siguiente artículo relacionado:
http://www.mim.cl/didactica-de-las-matematicas-en-el-contexto-de-los-mapas-de-progreso-y-los-ajustes-curriculares/prontus_mim/2011-11-17/175601.html
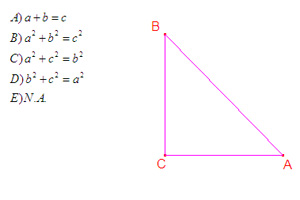







 Sorpresa de Yerbas Buenas
Sorpresa de Yerbas Buenas